Propagation & Interactions

Propagation

The propagation section is used to describe the physical process which is associated with the movement of a particle, and also the means by which the equations of motion are solved. The equations of motions are solved numerically with various control methods for the time step used during integration of a specific particle trajectory. The abstract base class of all particle trajectories is KSTrajectory.

There are essential five different equations of motion (trajectories) available for particle tracking in Kassiopeia. These are, exact, adiabatic, electric, magnetic, and linear. These are implemented in GitHub: Kassiopeia/Trajectories and some specialized classes exist for spin particles.

Exact trajectory

The first trajectory type is the so-called exact method, which solves the Lorentz equation for charged particles exactly without any approximations. It is visualized below:

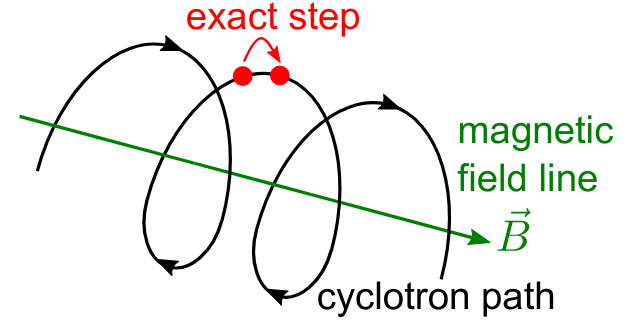
Adiabatic trajectory

The second method is the adiabatic method, which is useful for solving charged particle motion in the presence of smoothly varying magnetic fields. In this case, only the motion of the “guiding center” (a point on the magnetic field line) is computed, which allows certain approximations. One may then reconcstruct the cyclotron motion of the particle around the field line, however this is entirely optional. This method is visualized below:

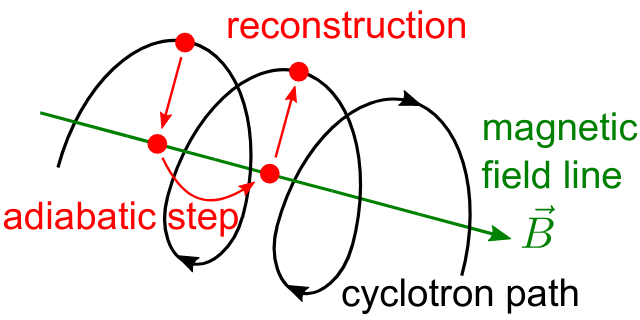
Electric and magnetic trajectories

The next two types, electric and magnetic (not shown here), are used for tracking the field lines of static electric and magnetic fields respectively. Finally, the linear trajectory calculates a linear motion that is independent of any external fields.

The definition of a trajectory for the simulation is usually combined with additional parameters that define the behavior of the simulation:

The integrator is responsible for solving the differential equation (ODE) in order to perform the tracking. Integrators are based off the class KSMathIntegrator.
An interpolator allows to speed up the ODE solving, by interpolating the particle’s parameters over a single step. Typically, the ODE solver performs evaluations of the particle state in between the initial and final position, which is time-consuming. Interpolators are based off the class KSMathIntegrator.
Additional terms extend the differential equation of the base trajectory. For example in case of the adiabatic trajectory, one may add terms for gyration or drift that are otherwise not included in the appoximation. The ODE terms are based off the class KSMathDifferentiator.
Additional controls can modify the step size. Options exist for a static setting (e.g. a step size of 1 mm) or dynamic adjustment (e.g. a step size derived from the local magnetic field.) Step controls are based off the class KSMathControl. Multiple controls can be combined, in which case the smallest possible step is taken.

Trajectory types

The tables below lists the available integrators, interpolators, and terms:

Trajectory integrators
Name	XML Element	Solution Order	Function evaluations	Error estimate	Description
RKF54	`integrator_rk54`	5	6	Yes	5th/4th-order Runge-Kutta
RKDP54	`integrator_rkdp54`	5	7	Yes	5th-order Runge-Kutta, 4th-order dense output
RK65	`integrator_rk65`	6	8	Yes	6th/5th-order Runge-Kutta
RKF8	`integrator_rk8`	8	13	No	8th-order Runge-Kutta
RK86	`integrator_rk86`	8	12	Yes	8th/6th-order Runge-Kutta
RK87	`integrator_rk87`	8	13	Yes	8th/7th-order Runge-Kutta
RKDP853	`integrator_rkdp853`	8	16	Yes	8th-order Runge-Kutta, 7th-order dense output
Sym4	`integrator_sym4`	4	4	No	4th-order Symplectic; only for exact tracking

Trajectory interpolators
Name	XML Element	Description
Fast	`interpolator_fast`	Fast linear interpolation
Hermite	`interpolator_hermite`	Hermite polynomial interpolation
Cont. Runge-Kutta	`kstraj_interpolator_crk`	Continuous Runge-Kutta (needs dense output)

Trajectory terms
Name	XML Element	Description
Propagation	`term_propagation`	Basic particle propagation
Constant Force	`term_constant_force_propagation`	Propagation by constant force
Synchrotron	`term_synchrotron`	Energy loss from synchrotron radiation
Drift	`term_drift`	Electromagnetic field drifts, adiabatic only
Gyration	`term_gyration`	Gyration around guiding center; adiabatic only
Gravity	`term_gravity`	Gravity pull; exact only

Trajectory controls
Name	XML Element	Description
Length	`control_length`	Fixed length
Time	`control_time`	Fixed time
B-Field Gradient	`control_B_change`	Length scaled by relative B-field gradient
Cyclotron	`control_cyclotron`	Length scaled to length of a full cyclotron turn
Energy	`control_energy`	Length adjusted to limit total energy violation
Magnetic Moment	`control_magnetic_moment`	Length adjusted to limit adiabaticity violation
Momentum Error	`control_momentum_numerical_error`	Length adjusted to limit momentum error
Position Error	`control_position_numerical_error`	Length adjusted to limit position error
Spin M-Dot	`control_m_dot`	Length scaled by $dot{M}$ (spin tracking only)
Spin Precession	`control_spin_precession`	Length scaled by precession freq. (spin tracking only)

Examples

The exact tracking method can be used where accuracy is of the utmost importance, but requires a large number of steps in order propagate a particle for a long time or distance. An example of its use is given below:

<kstraj_trajectory_exact name="trajectory_exact" attempt_limit="8">
    <interpolator_crk name="interpolator_crk"/>
    <integrator_rkdp853 name="integrator_rkdp853"/>
    <term_propagation name="term_propagation"/>
    <control_position_error name="control_position_error" absolute_position_error="1e-12" safety_factor="0.75" solver_order="8"/>
    <control_length name="stepsizelength" length="1e-4" />
    <control_time name="stepsizetime" time="1e-6" />
</kstraj_trajectory_exact>

In the above example, the integrator type specified integrator_rkdp853 is an 8-th order Runge-Kutta integrator with a 7-th order dense output interpolant (specified by interpolator_crk). The step size control is accomplished through the combination of three different methods. Two of them, control_length and control_time, place a fixed limit on the step size, while the third control_position_error dynamically attempts to limit the local numerical error on the particle’s position. In this case no additional terms besides basic propagation are defined, since the exact trajectory does not make any approximations.

All of the trajectories take an optional parameter attempt_limit which limits the number of tries an integration step will be re-attempted if a step size control determines that the step has failed. The default number of maximum number of attempts is 32. If a trajectory makes no progress after the maximum number of allowed attempts, the track will be terminated with a trajectory_fail flag.

An example of the adiabatic trajectory with some additional options is specified in the following:

<!--  adiabatic trajectory -->
<kstraj_trajectory_adiabatic name="trajectory_adiabatic" piecewise_tolerance="1e-6" max_segments="130" use_true_position="true" cyclotron_fraction="{1.0/64.0}" attempt_limit="8">
    <interpolator_crk name="interpolator_crk"/>
    <integrator_rkdp853 name="integrator_rkdp853"/>
    <term_propagation name="term_propagation"/>
    <term_drift name="term_drift"/>
    <term_gyration name="term_gyration"/>
    <control_time name="control_time_adiab" time="1e-6"/>
    <control_position_error name="control_position_error" absolute_position_error="1e-9" safety_factor="0.75" solver_order="8"/>
</kstraj_trajectory_adiabatic>

In this example, both the motion of the particle’s guiding center drift (term_drift) and the particle’s local gyration (term_gyration) itself are included in the equations of motion. If the second term is not present, the adiabatic tracjectory only computes the movement of the guiding center. It is important to note that the adiabatic trajectory cannot be used if there is no magnetic field present. Similar to the example above, the step size is defined by a combination of two controls.

The last three trajectory types can be specfified as follows:

<!--  magnetic trajectory -->
<kstraj_trajectory_magnetic name="trajectory_magnetic" piecewise_tolerance="1e-12" max_segments="128">
    <interpolator_crk name="interpolator_crk"/>
    <integrator_rkdp54 name="integrator_rkdp54"/>
    <term_propagation name="term_propagation" direction="forward"/>
    <control_time name="control_time" time="1.e-4"/>
    <control_length name="control_length" length="1e-2"/>
</kstraj_trajectory_magnetic>

<!--  electric trajectory -->
<kstraj_trajectory_electric name="trajectory_electric" piecewise_tolerance="1e-12" max_segments="128">
    <interpolator_crk name="interpolator_crk"/>
    <integrator_rkdp54 name="integrator_rkdp54"/>
    <term_propagation name="term_propagation" direction="backward"/>
    <control_time name="control_time" time="1.e-4"/>
    <control_length name="control_length" length="1e-2"/>
</kstraj_trajectory_electric>

<kstraj_trajectory_linear name="trajectory_linear" length="1.e-8" />

The electric and magnetic field line trajectories are useful for visualization purposes, and during the design stages of an experiment or simulation. Note that in the above examples we have used a faster but less accurate Runge-Kutta integrator integrator_rkdp54. The property direction in term_propagation can be used to specify the direction in which field lines are tracked (positive-to-negative or north-to-south). The linear trajectory takes no parameters besides a fixed step length,.

In all of the trajectories (exact, adiabatic, electric, magnetic) the parameters piecewise_tolerance and max_segments are optional. They dictate how a particles trajectory (in between steps) should be approximated by piecewise linear segments when determining surface and volume intersections. These parameters are only used when the ksnav_meshed_space navigator is in use, and determine how accurately intersections are found. The default ksnav_space navigator ignores these parameters, since it uses a faster but less accurate approximation by linearly interpolating a particle’s intermediate state and position. See below for details on navigation.

The adiabatic trajectory also takes the additional parameters use_true_position and cyclotron_fraction when the mesh_spaced_navigator is in use. The parameter use_true_position determines whether the particle or its guiding center position is used for the purpose of finding intersections. If the particle’s true position is used, then the parameter cyclotron_fraction dictates the number of linear segments the semi-helical path is broken into.

Interactions

In between generation and termination, discrete stochastic interactions involving the particle of interest may be applied during tracking. These interactions are divided according to whether they are active in a volume, or on a surface. In both cases, the behavior ties with the KGeoBag module that provides the geometric information.

Volume Interactions

Volume interactions typically involve scattering off of a gas. The abstract base class of all volume interactions is KSSpaceInteraction. Simple situations where the scattering interactions is treated approximately by a constant density and cross section can be constructed as follows:

<ksint_scattering name="int_scattering" split="true">
    <density_constant temperature="300." pressure="3.e0"/>
    <calculator_constant cross_section="1.e-18"/>
</ksint_scattering>

In this example the density is computed according to the ideal gas law from the temperature (Kelvin) and pressure (Pascal) and the cross section is treated as a constant (independent of particle energy). Other forms of interaction are available in GitHub: Kassiopeia/Interactions. For more complicated interactions (e.g. involving differential or energy dependent cross sections) the user may need to devise their own interaction class. Volume interactions must always be associated with a particular volume when describing the simulation structure.

Surface Interactions

Surface interactions are much more limited in their scope and only occur when the track of a particle passes through a surface. The abstract base class of all surface interactions is KSSurfaceInteraction.

For example, to cause a particle to be reflected diffusely (Lambertian) from a surface the user can specify an interaction of the following type:

<ksint_surface_diffuse name="int_surface_diffuse" probability=".3" reflection_loss="0." transmission_loss="1."/>

Similarly, one may use the following code to employ fully specular reflection:

<ksint_surface_specular name="int_surface_diffuse" probability="0." reflection_loss="0." transmission_loss="1."/>

In order for this interaction to operate on any particles it must be associated with a surface in the simulation command structure.